모델 구조를 실험 중인데 모델 간 성능이 비슷해서 성능과 해석 가능성의 균형을 갖춘 최종 모델 을 선정하고자 함.
목적, 마감, 결과, subtasks
현재 프로젝트 상황
주의 분산 행동 분류별 중요한 지표 - Precision, Recall 중요
stacked lstm + attention code
모델 성능
| 모델 | train macro f1 | val macro f1 | test macro f1 | macro f1 train-val gap |
| stacked LSTM | 0.986 | 0.813 | 0.886 | 0.173 |
| Bi-LSTM | 0.952 | 0.849 | 0.902 | 0.103 |
| stacked LSTM + Attention | 0.938 | 0.872 | 0.887 | 0.066 |
| Bi-LSTM + Attention | 0.938 | 0.856 | 0.893 | 0.082 |
- 최종 Test 성능 기준
- Stacked-Bi-LSTM 모델의 Test F1 Macro 0.902로 가장 높음 → 성능 측면에서 최고
- 일반화 성능(Train-Val Gap)
- Stacked LSTM + Attention 모델이 Gap이 가장 작음 → 안정적으로 학습됨
- 과적합 여부
- Stacked LSTM은 과적합 매우 큼 → 실전 사용 부적합
Attention 모델들이 overfitting 적고 generalization 성능이 안정적
각 클래스별 성능
| 클래스 | 특징 및 관찰 |
| normal | 거의 모든 모델에서 high recall(0.93 ~ 0.98) |
| phonecall | 모든 모델에서 recall 1 수준, 특성이 분명함 |
| text | 모든 모델에서 가장 성능이 낮음 val/test에서 0.612 ~ 0.790 사이 모델이 가장 혼동함 |
| yawn | 모든 모델에서 val/test 성능 낮고 편차 있음 train 성능 대비 하락 |
- 가장 혼동되는 text, yawn precision, recall 비교
모델 Set Text
PrecisionText Recall Yawn
PrecisionYawn
RecallStacked LSTM Train 0.996 0.938 1.0 0.983 Val 0.722 0.531 0.803 0.646 Test 0.744 0.826 0.882 0.755 Stacked + Bi Train 0.93 0.862 0.967 0.932 Val 0.8 0.626 0.826 0.695 Test 0.833 0.843 0.852 0.784 Stacked LSTM+ Attn Train 0.738 0.748 0.95 0.695 Val 0.893 0.894 0.977 0.858 Test 0.691 0.881 0.937 0.748 Stacked + Bi + Attn Train 0.76 0.626 0.921 0.707 Val 0.91 0.854 0.963 0.897 Test 0.73 0.86 0.881 0.799 💡precision vs recall서비스 성격에 따라 선택 기준 달라져야 함
- 실시간 경고 서비스 → precision 우선(오경고 방지)
- 사후 리포트 분석 목적 → recall 우선(행동 놓치지 않기)
💡attention 계열 모델을 쓰니까 오히려 validation/test set의 성능이 train보다 더 좋은 현상이 관찰됨attention 계열 모델은 보통 dropout, early stopping, batch norm, weight decay, regularization 등을 함께 사용함
이 요소들은 train loss를 너무 줄이지 못하게 하면서 generalizaton(일반화)을 유도
→ 그래서 train에서는 일부 행동을 덜 학습하지만
→ validation/test에서는 오히려 과적합이 덜 된 효과로 더 잘 동작할 수 있음
모델 성능 해석
| 모델 | 설명 |
| Stacked LSTM | - LSTM만 쌓은 구조로 과적합이 발생하기 쉬움 - Backward 정보를 못 받아서 시간 흐름 이해 부족 → 졸음/문자 판단 어려움 - validatoin/test 에서 text, yawn 성능 급락 |
| Stacked + Bi | - 양방향 흐름 파악 가능 → 행동 패턴 인지력 상승 - precision, recall 모두 균형 잡힘 |
| Attention 계열 | - 특정 시점 중요도 학습 → Recall 상승 - 하지만 전체적 맥락보다는 특정 순간 강조 → Precision 감소 경향 |
Attention 없이 LSTM 해석하기: Integrated Gradients, LIME, SHAP 등
| 설명 | 예시 | |
| Integrated Gradients | 모델 예측에 대해 입력 특성이 기여한 정도를 수치적으로 계산해주는 해석 방식 | |
| LIME | 입력 시퀀스를 구성하는 feature에 국소적인 해석을 제공 모델 예측 주위의 근방에서 입력 일부를 변화시키며 예측 변화를 관찰해 각 부분의 중요도를 추정 | 텍스트 분류 모델이 특정 문장에서 어떤 단어들이 분류 결정에 긍정/부정적으로 작용했는지 가중치 형태로 나타낼 수 있음 |
| SHAP | 각 입력 요소의 기여도를 일관성 있는 값으로 산출하여 feature importance를 제공 SHAP은 계산 비용이 높고, sequence 모델에선 처리 시간이 오래 걸릴 수 있음 | 시계역 예측 LSTM에서 각 시점의 입력이 결과에 미친 영향력을 정량화할 수 있음 |
IG vs SHAP vs LIME
- timestep도 해석하려면 IG
- 추가로 SHAP도 병행해서 사용하면 더 깊은 인사이트 얻을 수 있음
실제 IG + SHAP 조합을 많이 사용
Attention vs Integrated Gradietns(IG)
| 구분 | Attention | Integrated Gradients(IG) |
| 언제 사용되나? | 모델 안에 포함되어 학습됨 (학습 중 작동) | 모델 밖에서 학습 후에 해석할 때 사용 (학습 후 작동, 사후 해석) |
| 무엇을 보여줌? | 입력의 시점(시간) 중 어떤 부분에 집중했는가 | 입력의 특성(변수) 중 어떤 것이 예측에 기여했는가 |
| 누가 계산? | 모델이 학습하면서 직접 계산 | 사람이 captum 같은 도구로 계산 |
| 시점별 해석 가능? | 가능(Attention weight) | 가능(Time x Feature importance matrix) |
| 해석 대상 | 보통 time step | 보통 feature(ex. mar, yaw, pitch) |
| 한 줄 요약 | 모델은 언제 집중했지? | 무엇 때문에 그렇게 예측했지? |
Attention
중요한 시점을 가중치 로 강조핵심 개념
- 모델이 sequence 중 어느 시점의 정보를 얼마나 반영할지 가중치를 부여
→ 이 가중치는 학습됨
- 각 시점의 hidden state를 가중 평균해서 하나의 context vector로
context = Σ (attention_weight_t × hidden_state_t)
LSTM과는 어떻게 연결되고 학습되는지
- LSTM은 각 시점의 정보를 요약한
hidden state를 출력
- Attention은 이
hidden state들을 받아 “어떤 시점이 중요했는지” 판단score_t = tanh(W_attn · h_t) # 각 시점마다 score를 계산 attn_weight_t = softmax(score_t) # 모든 시점에 대해 softmax로 정규화
- 최종 context vector를 만들어 classification 에 사용
context = Σ (attn_weight_t × h_t) # 중요도를 반영한 시점별 가중 평균
- 예측 결과 기반으로 loss 계산 후 attention 도 함께 업데이트
Attention도 네트워크의 일부이기 때문에,
전체 모델의 loss(ex. CrossEntropyLoss)를 기준으로
Attention Layer의 파라미터(W_attn, V, 등)도 역전파로 같이 학습됨
즉,
- “이 시점을 더 보라고 가중치를 높이면 loss가 줄더라”
이런 방향으로 attention weight를 업데이트 함
Integrated Gradients
출력이 얼마나 변하는지를 추적
핵심 개념
💡
이 feature를 천천히 0에서 원래 값으로 바꿔볼 때, 출력(logit)이 얼마나 변하더라?
→ 이 변화량을 적분(gradient 누적)해서 feature 별 중요도를 구함
feature 값들을 baseline(ex. 0) → 입력(ex. mar=0.3, pitch=0.7)으로 조금씩 바꾸며 모델 출력이 얼마나 민감하게 바뀌는지를 추적
Attention, IG 시각화 예시
각 클래스별 예측 라벨 == 정답 라벨인 샘플들 하나씩 뽑아서 attention weight 시각화
각 클래스별 예측 라벨 == 정답 라벨인 샘플을 하나씩 뽑아서 ig attribution 시각화
각 클래스별 예측 라벨 != 정답 라벨인 샘플들 하나씩 뽑아서 attention weight 시각화
각 클래스별 예측 라벨 != 정답 라벨인 샘플을 하나씩 뽑아서 ig attribution 시각화
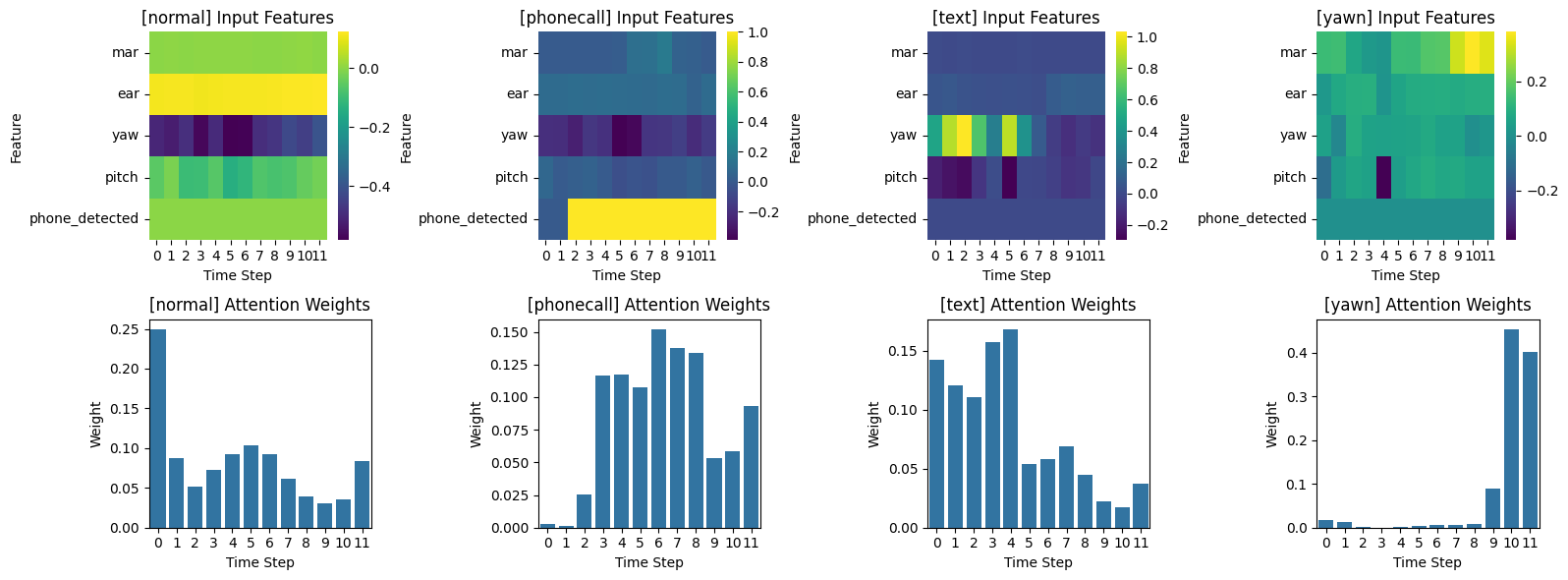
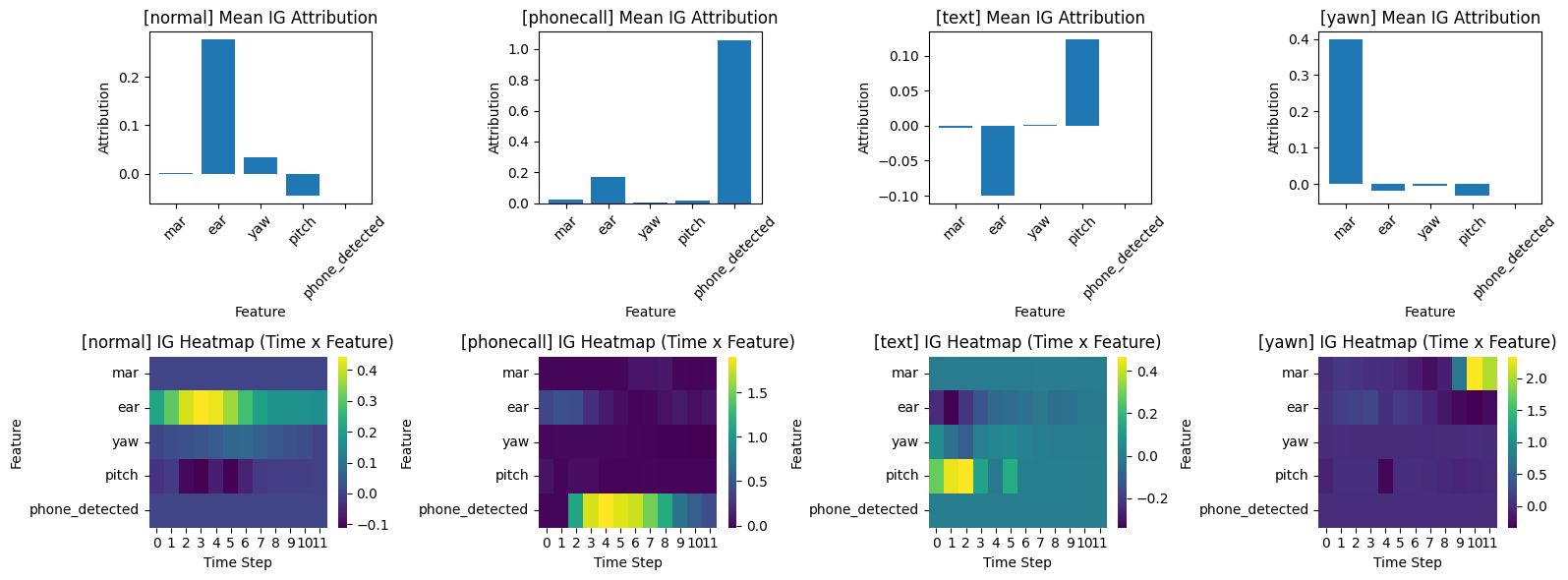
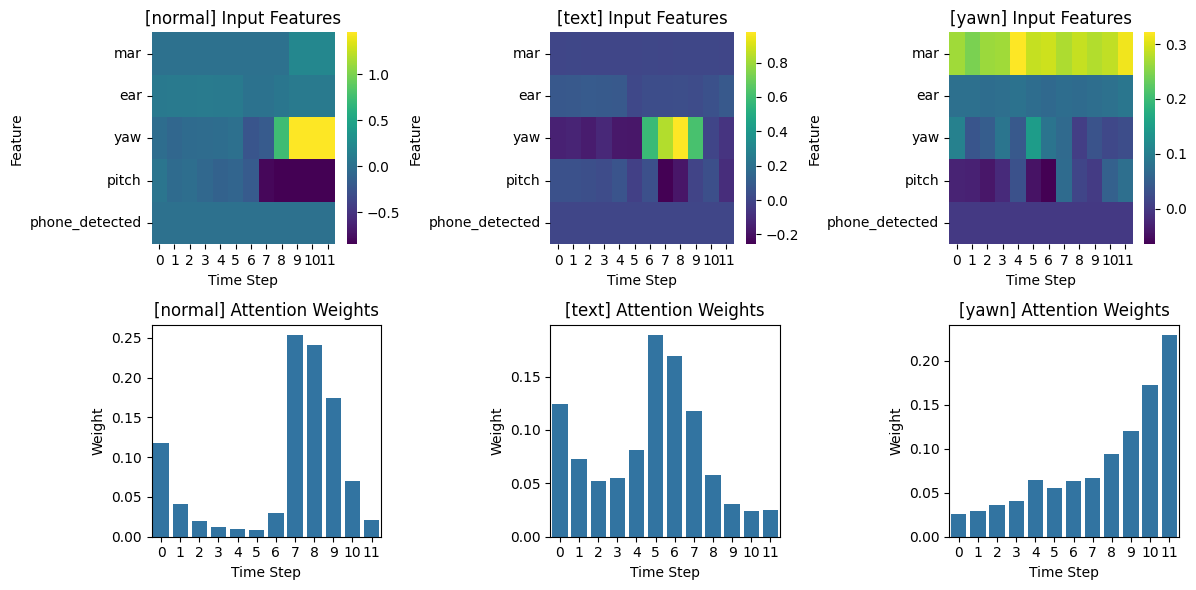
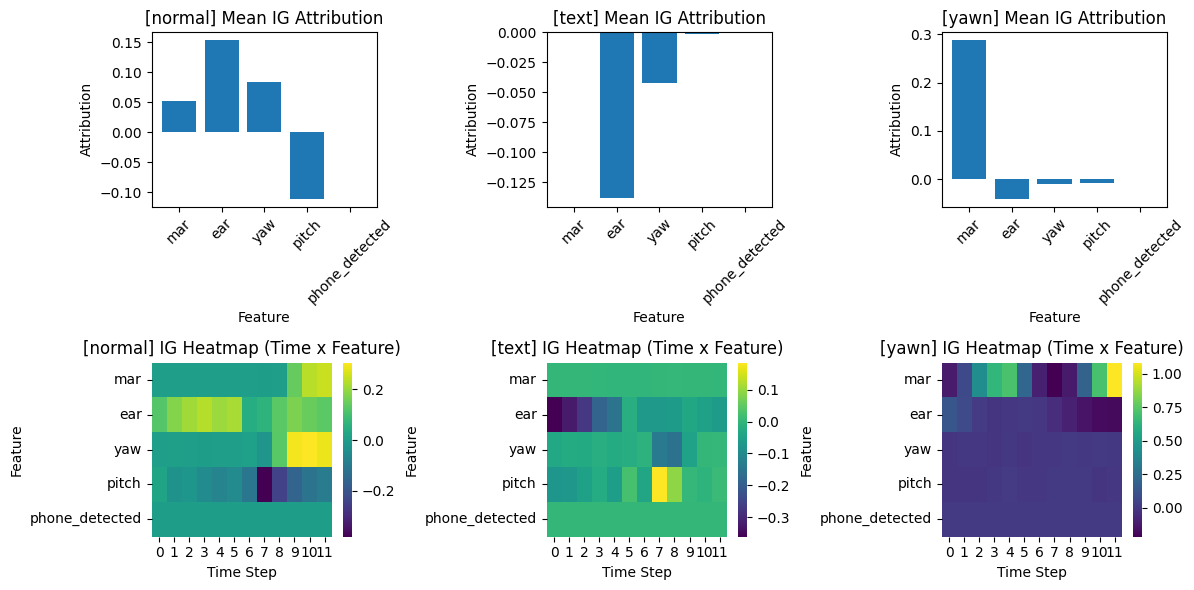
IG Attribution 해석 방식
| attribution 부호 | |
| 양수 | 해당 feature 가 정답 class로 예측하는 데 도움이 됨 |
| 음수 | 해당 feature 가 정답 class로 예측되는 것을 방해함 (다른 클래스로 끌어감) |
Global-level로는 어떻게 해석할까?
attention weight, ig attribution를 각 시점별로 평균 내서 해석해볼 수 있음
예측 == 정답인 샘플들의 global-level 해석
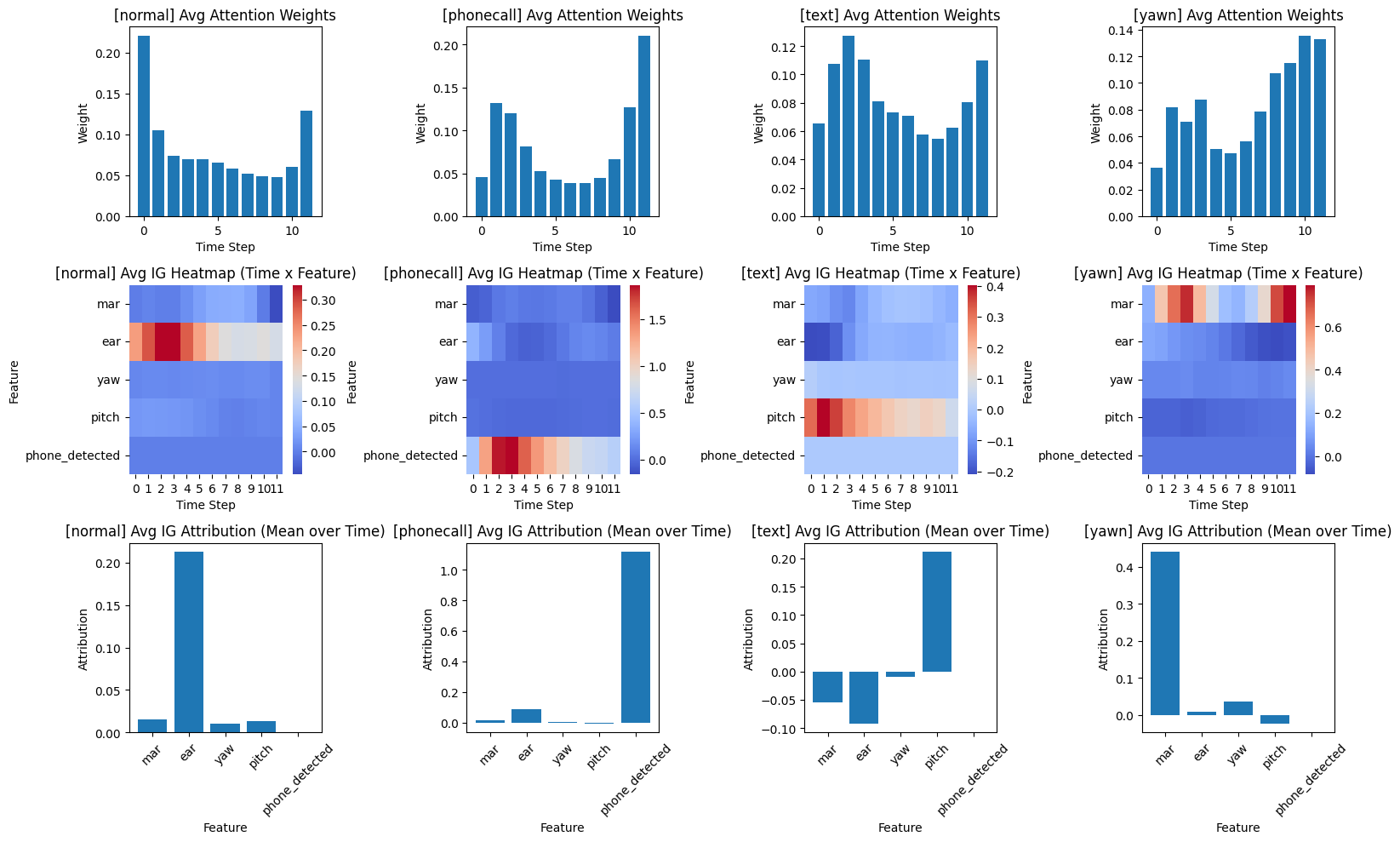
- 잘못 분류한 샘플을 해석할 때는 잘 분류한 Ig, attention global-level 값과 비교하는 게 좋을 듯
- ig, attention global-level 값을 시각화할 때는 boxplot 등 각 time step 별 분포를 보는 게 좋을 듯